
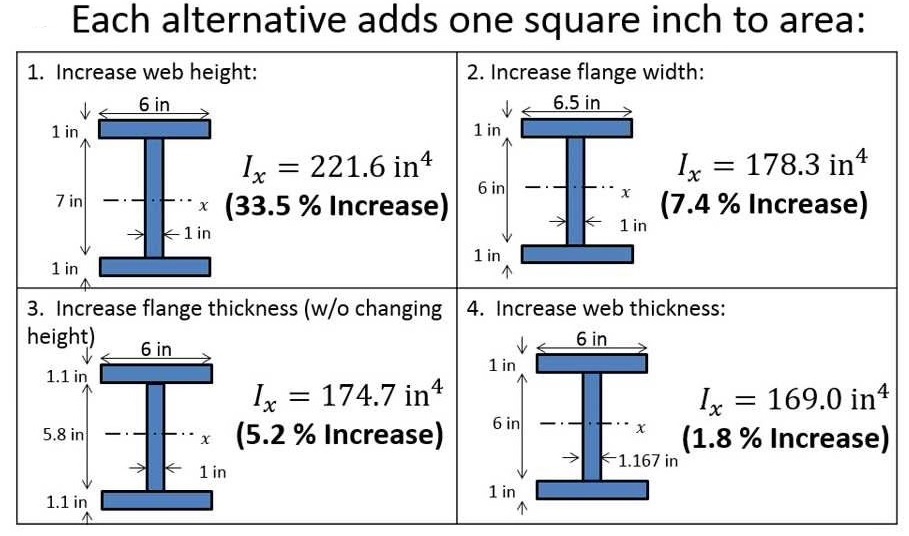
Last … In the ULS (ultimate limit state) Design we verify the stresses in the steel members due to bending, shear, normal forces and buckling. E is modulus of elasticity (steel is 29,000,000) i is moment of inertia (22. This will make it easier for you to … Suppose a section of steel angle is used to support a structural beam, which would otherwise have no available bearing, as in the following sketch. For aeronautical and space applications where designs must be much less conservative for weight saving, structural testing is often required to ensure safety as reliance on structural analysis alone is more difficult (and expensive) to justify.Steel beam load capacity calculator.
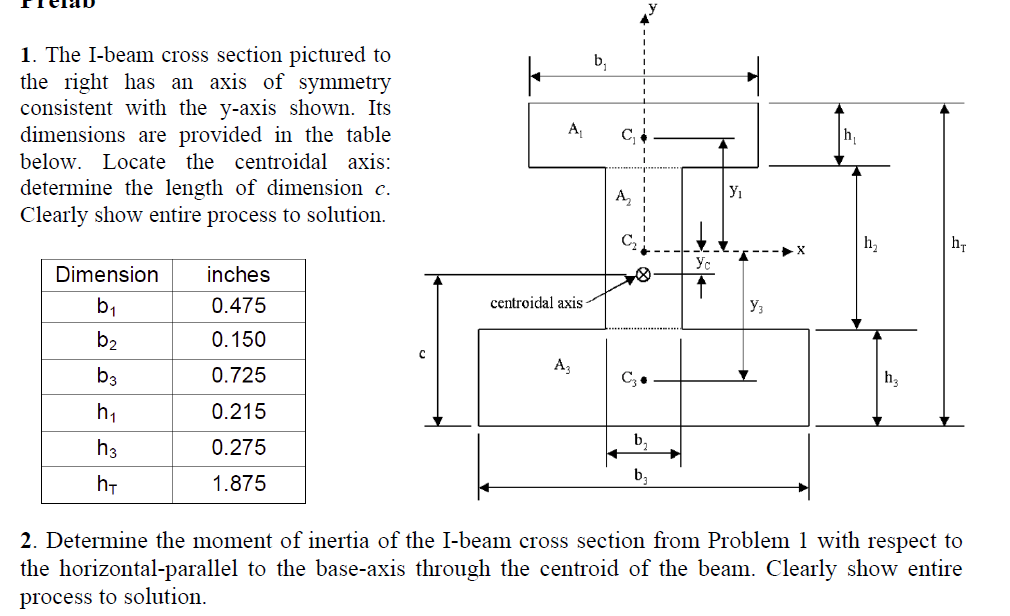

There may also be a number of different critical cases that require consideration, such as there being different values for orthogonal and principal axes and in the case of unequal angle sections in the principal axes there is a section modulus for each corner.įor a conservative (safe) design, civil structural engineers are often concerned with the combination of the highest load (tensile or compressive) and lowest elastic section modulus for a given section station along a beam, although if the loading is well understood one can take advantage of different section modulus for tension and compression to get more out of the design. In this case F/T buckling must still be assessed as the beam length and restraints may result in reduced compressive member bending allowable stress or capacity. In the case of T-sections if there are tensile fibres at the bottom of the T they may still be more critical than the compressive fibres at the top due to a generally much larger distance from the neutral axis so despite having a higher allowable stress the elastic section modulus is also lower. Generally (except for brittle materials like concrete) tensile extreme fibres have a higher allowable stress or capacity than compressive fibres. Though generally section modulus is calculated for the extreme tensile or compressive fibres in a bending beam, often compression is the most critical case due to onset of flexural torsional (F/T) buckling. ( January 2014) ( Learn how and when to remove this template message) Unsourced material may be challenged and removed. Please help improve this section by adding citations to reliable sources. Shape factor for a rectangular section is 1.5. Section modulus equations Cross-sectional shape It is also often used to determine the yield moment ( M y) such that M y = S ⋅ σ y, where σ y is the yield strength of the material. It is often reported using y = c, where c is the distance from the neutral axis to the most extreme fibre, as seen in the table below. The elastic section modulus is defined as S = I / y, where I is the second moment of area (or area moment of inertia, not to be confused with moment of inertia) and y is the distance from the neutral axis to any given fibre. Eurocode 3 (EN 1993 - Steel Design) resolves this by using W for both, but distinguishes between them by the use of subscripts - W el and W pl.įor general design, the elastic section modulus is used, applicable up to the yield point for most metals and other common materials. Elastic modulus is S in North America, but Z in Britain/Australia, and vice versa for the plastic modulus. North American and British/Australian convention reverse the usage of S & Z. The section moduli of different profiles can also be found as numerical values for common profiles in tables listing properties of such. There are two types of section moduli, the elastic section modulus and the plastic section modulus. Equations for the section moduli of common shapes are given below. Any relationship between these properties is highly dependent on the shape in question. Other geometric properties used in design include area for tension and shear, radius of gyration for compression, and second moment of area and polar second moment of area for stiffness. Section modulus is a geometric property for a given cross-section used in the design of beams or flexural members. JSTOR ( October 2009) ( Learn how and when to remove this template message).Please help improve this article by adding citations to reliable sources. This article needs additional citations for verification.


 0 kommentar(er)
0 kommentar(er)
